考研数学二（一元函数微分学的应用（二）——中值定理、微分等式与微分不等式与一元函数微分学的应用（三）——物理应用）模拟试卷1

考研数学二（一元函数微分学的应用（二）——中值定理、微分等式与微分不等式与一元函数微分学的应用（三）——物理应用）模拟试卷1

选择题

1.设函数f(x)=x(2x-3)(4x-5)，则方程f’(x)=0的实根个数为（ ）．(C)

A. 0

B. 1

C. 2

D. 3

解析：f(x)=0的实根为x₁=0，x₂=5/4，x₃=3/2，即 f(0)=f(5/4)=f(3/2)，且f(x)可导，则由罗尔定理，存在ξ₁∈(0，5/4)，使f’(ξ₁)=0；存在ξ₂∈(5/4，3/2)，使f‘(ξ₂)=0．故f’(x)=0至少有两个实根．又f’(x)=0为一元二次方程，至多有两个实根．综上，选(C)．

2.若方程x-elnx-k=0在(0，1]上有解，则k的最小值为（ ）．(C)

A. -1

B. 1/e

C. 1

D. e

解析：记f(x)=x-elnx—k，则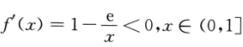，这表明f(x)在(0，1]上单调递减，因而它在(0，1]上最多只有一个零点．

又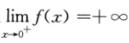，由极限的保号性，存在r，0＜r＜1，使得f(r)＞0．f(x)在[r，1]上连续，f(r)＞0，f(1)=1-k．

当f(1)=1-k=0，即k=1时，x=1是f(x)的一个零点，即x=1是方程x-eln x-k=0的一个解．

当f(1)=1-k＜0，即k＞1时，由在闭区间上连续函数的零点定理，知函数f(x)在(r，1)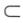

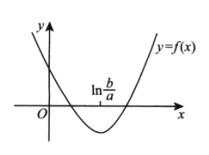
3.设函数f(x)=ae^x-bx(a＞0)有两个零点，则b/a的取值范围是（ ）.(D)

A. (0，1/e)

B. (0，e)

C. (1/e，+∞)

D. (e，+∞)

解析：f(x)的定义域为(-∞，+∞)．

显然b＞0，否则f(x)是单调增加函数，与条件矛盾．

f’(x)=ae^x-b，令f’(x)=0，得驻点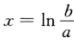

当x∈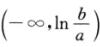时，f’(x)＜0，则f(x)单调递减．

当x∈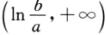时，f’(x)＞0，则f(x)单调递增．

当x→-∞时，f(x)→+∞．当x→+∞时，f(x)→+∞．

因此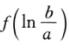是最小值．故当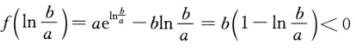时，f(x)有两个零点(见图)，此时b/a＞e，即b/a∈(e，+∞)．

4.已知函数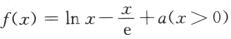(D)

A. (-1，0)

B. (0，1)

C. (-∞，0)

D. (0，+∞)

解析：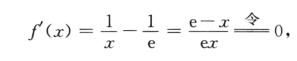

5.设函数f(x)在[a，+∞)(a＞0)上一阶导数连续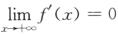，，则（ ）．

(C)

A.

B.

C.

D.

解析：由拉格朗日中值定理知，

f(x+1)-f(x)=f’(ξ)，x＜ξ＜x+1，

故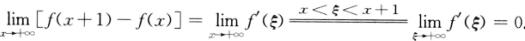

(C)正确．

取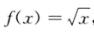，则

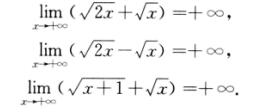
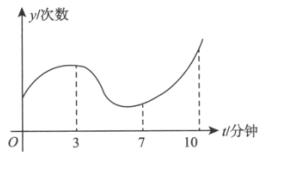
6.设二阶可导函数y=f(t)表示某人在10分钟内心跳次数的变化曲线，如图所示．则关于此人心跳次数的增长速度，说法正确的是（ ）．

(

本文档预览：3000字符，共8615字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载