考研数学二（一元函数积分学的概念与性质、微分方程）模拟试卷1

考研数学二（一元函数积分学的概念与性质、微分方程）模拟试卷1

选择题

1.设函数f(x)在区间[0，1]上连续，则∫₀¹f(x)dx=（ ）．

(B)

A.

B.

C.

D.

解析：方法一 若函数f(x)在区间[0，1]上连续，由定积分的定义，对任意的划分

T：0=x₀＜x₁＜…＜x_n=1，

以及任意的ξ_k∈[x_k-1，x_k](1≤k≤n)，均有

∫₀¹f(x)dx=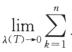f(ξ_k)△x_k，

其中△x_k=x_k-x_k-1，

只有选项(B)中，分割T是将区间[-0，1]作n等分，点ξ_k=为各个小区间的内点，区间长度为1/n，计算结果为∫₀¹f(x)dx．

故选(B)．

方法二 作为选择题，本题也可以利用特殊值法得到正确答案．

取f(x)=1，则∫₀¹ f(x)dx=1，而

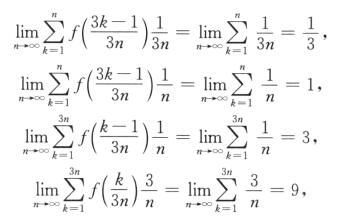
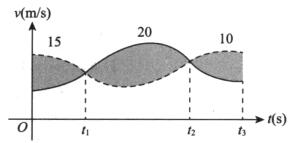
2.甲、乙两人赛跑，图中实线和虚线分别为甲和乙的速度曲线(单位：m／s)，三块阴影部分面积依次为15，20，10，且当t=0时，甲在乙前面10 m处，则在[0，t₃]上，甲、乙相遇的次数为（ ）．

(B)

A. 1

B. 2

C. 3

D. 4

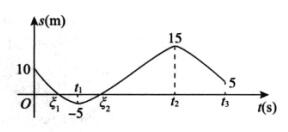
解析：设t时刻甲在乙前面s m处，由题图，可画出s=s(t)的大致图形，如图所示，从而可知s(0)=10＞0，s(t₁)=-5＜0，s(t₂)=15＞0，s(t₃)=5＞0，由问题的实际意义可知，s(t)为连续函数，故由零点定理，有s(ξ₁)=s(ξ₂)=0(ξ₁∈(0，t₁)，ξ₂∈(t₁，t₂))，即在[0，t₃]上，甲、乙相遇的次数为2．

3.设M=∫_-1/2^1/2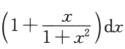．N=∫₀¹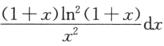，K=∫₀¹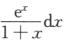(C)

A. M＞N＞K

B. N＞K＞M

C. K＞M＞N

D. K＞N＞M

解析：M=∫_-1/2^1/21dx+∫_-1/2^1/2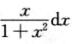，因为∫_-1/2^1/2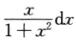=0，所以M=1．

令g(x)=(1+x)ln²(1+x)-x²(0≤x≤1)，则有

g‘(x)=ln²(1+x)+(1+x)2ln(1+x)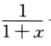-2x=ln²(1+x)+2ln(1+x)-2x．

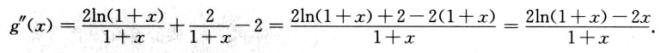
4.设f(x)是(0，+∞)内的正值连续函数，且f’(x)＜0，g(x)=∫₁^xf(t)dt，则g(1/2)和g(3/2)的可能取值是（ ）．(A)

A. -2，1

B. -2，3

C. 2，-1

D. 2，-3

解析：由于f(x)是(0，+∞)内的正值连续函数

本文档预览：3000字符，共15169字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载