考研数学（数学一）模拟试卷773

考研数学（数学一）模拟试卷773

选择题

1.设{α_n)为非零数列，下列命题正确的是( )．

D

解析：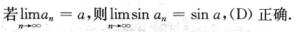

对于A，B选项，取α_n=2nπ，则sin α_n=0，arcsin(sin α_n)=0，{sin α_n}，{arcsin(sin α_n)}均收敛，但{α_n}发散．

对于C选项，取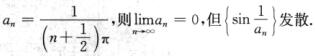

2.设函数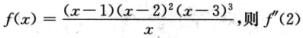(D)

A. 2

B. —2

C. 1

D. —1

解析：令g(x)=x^—1(x—3)³(x—1)，则f(x)=g(x)(x—2)²，

f’(x)=g’(x)(x—2)²+2(x—2)g(x)，

f’’(x)=(x—2)²g’’(x)+2(x—2)g’(x)+2(x—2)g’(x)+2g(x)，

故f’’(2)=2g(2)=—1．

3.已知级数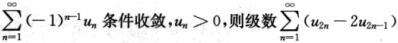(A)

A. 发散

B. 绝对收敛

C. 条件收敛

D. 敛散性无法判断

解析：

4.设空间曲面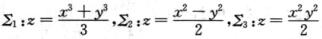(B)

A. S₁＞S₂＞S₃

B. S₂＞S₁＞S₃

C. S₃＞S₁＞S₂

D. S₃＞S₂＞S₁

解析：由于

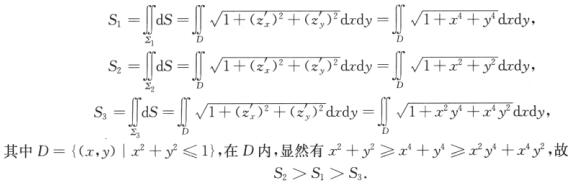
5.已知α₁，α₂，α₃，α₄是3维非零列向量，则下列命题

①若α₄可由α₁，α₂，α₃线性表示，则α₁，α₂，α₃+α₄线性无关；

②若α₄可由α₁，α₂，α₃线性表示，则r(α₁+α₂，α₂，α₃)=r(α₁，α₂，α₃，α₄)；

③若α₄不能由α₁，α₂，α₃线性表示，则α₁，α₂，α₃线性相关；

④若α₄不能由α₁，α₂，α₃线性表示，则2≤r(α₁，α₂，α₃，α₄)≤3．

正确命题的个数为( )．(C)

A. 1

B. 2

C. 3

D. 4

解析：因α₁，α₂，α₃，α₄是3维列向量，所以有r(α₁，α₂，α₃)≤3，r(α₁，α₂，α₃，α₄)≤3．

对于①，若α₁=α₂=α₃=α₄，则α₄可由α₁，α₂，α₃线性表示，但α₁，α₂，α₃+α₄线性相关。错误．

对于②，若α₄可由α₁，α₂，α₃线性表示，则有r(α₁，α₂，α₃)=r(α₁，α₂，α₃，α₄)，且r(α₁+α₂，α₂，α₃)=r(α₁，α₂，α₃)，故r(α₁+α₂，α₂，α₃)=r(α₁，α₂，α₃，α₄)．

对于③，如果α₁，α₂，α₃线性无关，则α_{4本文档预览：3000字符，共9688字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载}