考研数学三（无穷级数）模拟试卷47

考研数学三（无穷级数）模拟试卷47

选择题

1.设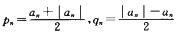，n＝1，2，…，则下列命题正确的是________．

(B)

A.

B.

C.

D.

解析：若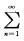a_n条件收敛，则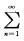|a_n|发散，由级数的性质知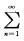p_n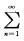，q_n都发散，排除选项A，C；若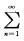a_n绝对收敛，则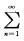a_n收敛，由级数的性质知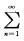p_n，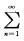

填空题

2.计算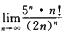

0

解析：应用级数收敛的必要条件.

考虑级数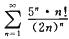，应用正项级数的比值审敛法有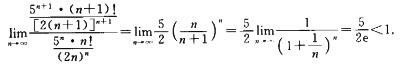

故级数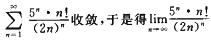

解答题

3.已知a_n＝∫₀¹x²(1－x)ⁿdx，(n＝1，2，…)证明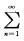

[*]

所以[*]a_n的敛散性应与[*]一致，所以[*]a_n收敛.

[*]

故[*]＝1／6．

解析：

4.设有两条抛物线y＝nx²＋1／n和y＝(n＋1)x²＋1／(n＋1)，记它们交点的横坐标的绝对值为a_n.

(1)求这两条抛物线所围成的平面图形的面积S_n；

(2)求级数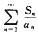

由y＝nx²＋1／n与y＝(n＋1)x²＋1／(n＋1)得a_n＝[*]

因图形关于y轴对称，所以

[*]

解析：

从点P₁(1，0)作x轴的垂线，交抛物线y＝x²于点Q₁(1，1)，再从Q₁作这条抛物线，的切线与x轴交于P₂，然后又从P₂作x轴的垂线，交抛物线于点Q₂，依次重复上述过程得到一系列的点P₁，Q₁；P₂，Q₂；…；P_n，Q_n；……(如图所示)

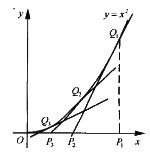
5.求

由y＝x²，得y’＝2x，对于任意a(0＜a≤1)，抛物线y＝x²在点(a，a²)处的切线方程为

y－a²＝2a(x－a)

且该切线与x轴的交点为(a／2，0)，故由[*]＝1，可见

[*]

解析：

6.求级数的和，其中n(n≥1)为自然数，而

由于[*]

本文档预览：3000字符，共10581字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载