考研数学一（常微分方程）模拟试卷33

考研数学一（常微分方程）模拟试卷33

选择题

1.设非齐次线性微分方程y’＋P(x)y＝Q(x)有两个不同的解y₁(x)，y₂(x)，C为任意常数，则该方程的通解是________．(B)

A. C[y₁(x)－y₂(x)]

B. y₁(x)＋C[y₁(x)－y₂(x)]

C. C[y₁(x)＋y₂(x)]

D. y₁(x)＋C[y₁(x)＋y₂(x)]

解析：由线性微分方程解的性质及结构知，C[y₁(x)－y₂(x)]必为原方程对应齐次线性微分方程的通解，所以，原微分方程的通解为y₁(x)＋C[y₁(x)－y₂(x)].

故应选B.

2.设线性无关函数y₁(x)，y₂(x)，y₃(x)都是二阶非齐次线性方程y”＋P(x)y’＋Q(x)y＝f(x)的解，C₁，C₂是任意常数，则该非齐次方程的通解是________．(D)

A. C₁y₁－C₂y₂＋y₃

B. C₁y₁＋C₂y₂－(C₁＋C₂)y₃

C. C₁y₁＋C₂y₂－(1－C₁－C₂)y₃

D. C₁y₁＋C₂y₂＋(1－C₁－C₂)y₃

解析：因为y₁、y₂以都是非齐次方程的解，所以其差y₁－y₃，y₂－y₃是对应齐次方程的解，又由于y₁，y₂，y₃线性无关.所以y₁－y₃与y₂－y₃也线性无关，故由线性方程组解的结构定理，，对应齐次方程的通解C₁(y₁－y₃)＋C₂(y₂－y₃)再加上非齐次方程的一个特解就是非齐次方程

通解.

故应选D.

3.设y₁、y₂是二阶常系数线性齐次方程y”＋p(x)y’＋q(x)y＝0的两个特解，则由y₁(x)与y₂(x)能构成该方程的通解，其充分条件为________．(B)

A. y₁(x)y’₂(x)－y₂(x)y’₁(x)＝0

B. y₁(x)y’(x)－y₂(x)y’₁(x)≠0

C. y₁(x)y’₂(x)＋y₂(x)y’₁(x)＝0

D. y₁(x)y’(x)＋y₂(x)y’₁(x)≠0

解析：由题意知y₁(x)与y₂(x)线性无关，即y₂(x)／y₁(x)≠C．

求导得，

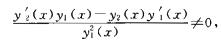
填空题

4.微分方程xy”＋3y’＝0的通解为________．

y＝C₁＋C₂／x²

解析：令y’＝p，则y”＝dp／dx.

代入原方程得xdp／dx＋3p＝0，分离变量得dp／p＝－3dx／x，

两边积分得lnp＝－31nx＋lnC’₂，即p＝C’₂x^－3也即y’＝C’₂x^－3，解得y＝C₁＋C₂／x².

故应填y＝C₁＋C₂／x².

5.微分方程xy”＋(y’)²＝0满足初始条件y|_x＝0＝l，y’|_x＝0＝1／2的特解是________．

y＝[*]或y²＝x＋1

解析：令y’＝p，y”＝pdp／dy，则原方程化为

1°p＝0得y’＝0，与已知矛盾；

2°p≠0时，有ydp／dy＋p＝0，解得p＝C₁／y

把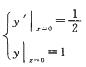代入得C₁＝1／2，即微分方程为y’＝1／2y．

解得y²＝x＋C₂，把y｜本文档预览：3000字符，共14616字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载