考研数学一（高等数学）模拟试卷395

考研数学一（高等数学）模拟试卷395

选择题

1.已知函数f(x)=1nx—x/e+α(x＞0)有两个零点，则α的取值范围是( )．(D)

A. (—1，0)

B. (0，1)

C. (—∞，0)

D. (0，+∞)

解析：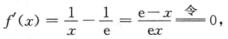

得x=e，又f”(x)=—1/x²＜0，故x=e是唯—极大值点，极大值为f(e)=α．

又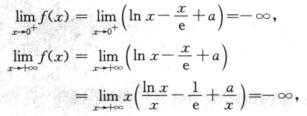

2.已知函数f(x)，g(x)可导，且f’(x)＞0，g’(x)＜0，则( )．(C)

A. ∫_—1⁰f(x)g(x)dx＞∫₀¹f(x)g(x)dx

B. ∫_—1⁰|f(x)g(x)|dx＞∫₀¹|f(x)g(x)|dx

C. ∫_—1⁰f[g(x)]dx＞∫₀¹f[g(x)]dx

D. ∫_—1⁰f[f(x)]dx＞∫₀¹g[g(x)]dx

解析：令f(x)=e^x，g(x)=e^—x，满足题干条件，但

∫_—1⁰f(x)g(x)dx=∫_—1⁰e^x·e^—xdx=∫₀¹e^x·e^—xdx=∫₀¹f(x)g(x)dx，

且

∫_—1⁰|f(x)g(x)|dx=∫_—1⁰|e^x·e^—x|dx=∫₀¹|e^x·e^—x|dx=∫₀⁰|f(x)g(x)|dx，

所以选项A，B错误．

令f(x)=x，g(x)=—x，亦满足题干条件，但

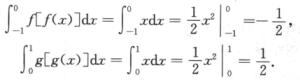
3.设函数f(x)满足，则( )．

(B)

A.

B.

C.

D.

解析：由于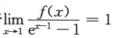，分母极限为0，则分子极限也为o，故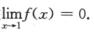

4.设f_n(x)=x^n—1e^1/x，n=1，2，…，x≠0，则f_n⁽ⁿ⁾(x)=( )．

(D)

A.

B.

C.

D.

解析：由函数列f_n(x)的表达式可知，当n=1时，f₁(x)=e^1/x，当n=2时，f₂(x)=x·e^1/x，…，

若要求f_n⁽ⁿ⁾(x)，可采用特殊值法，由f₁(x)=e^1/x，可得f’₁(x)=—1/x²·e^1/x，故当n=1时，选项中的表达式应为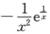

5.设{a_n}与{b_n}为两个数列，下列说法正确的是( )．

D

解析：A不正确，例如：a_n=2+(-1)ⁿ，b_n=2-(-1)ⁿ，显然{aⁿ}与{bⁿ}都发散，但aⁿbⁿ=3，显然{aⁿbⁿ}收敛；B、C都不正确，例如：aⁿ=n[1+(-1)ⁿ]，bⁿ=n[1-(-1)ⁿ]，显然{aⁿ}与{bⁿ}都无界，但aⁿbⁿ=0，显然{aⁿbⁿ}有界且

6.已知α＞0，则对于反常积分∫₀¹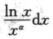(B)

A. 当

本文档预览：3000字符，共9700字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载