
考研数学一(高等数学)模拟试卷423
选择题
1.设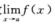 存在,
存在,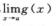 (D)
(D)
A. 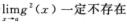 B.
B. 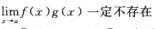 C.
C. 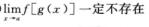 D.
D.  解析:取g(x)=|x|/x,
解析:取g(x)=|x|/x,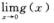 不存在,但
不存在,但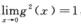 ,A错误;
,A错误;
取f(x)=x2,g(x)=sin1/x,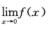 存在,
存在,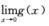 不存在,但
不存在,但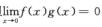 ,B错误;
,B错误;
取f(x)=cos x,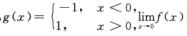 存在,
存在,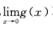 不存在,但
不存在,但
2.下列命题正确的是( ).(B)
A. 若|f(x)|在x=a处连续,则f(x)在x=a处连续
B. 若f(x)在x=a处连续,则|f(x)|在x=a处连续
C. 若f(x)在x=a处连续,则f(x)在x=a的一个邻域内连续
D. 若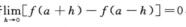 解析:令
解析:令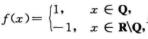 显然|f(x)|≡1处处连续,然而f(x)处处间断,A不正确;
显然|f(x)|≡1处处连续,然而f(x)处处间断,A不正确;
令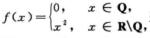 显然f(x)在x=0处连续,但在任意x=a≠0处函数f(x)都是间断的,故C不正确;
显然f(x)在x=0处连续,但在任意x=a≠0处函数f(x)都是间断的,故C不正确;
令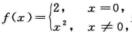 显然
显然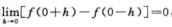 ,但f(x)在x=0处不连续,D不正确;
,但f(x)在x=0处不连续,D不正确;
若f(x)在x=a处连续,则
根据夹逼定理可知,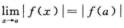
3.设f(x)连续,且g(x)=|x-a|[f(x)+|f(x)|],则g(x)在x=a处可导的充要条件是( ).(C)
A. f(a)=0
B. f’(a)=0
C. f(a)=-|f(a)|
D. f(a)=|f(a)|
解析:由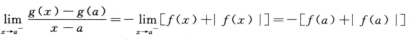 得
得
g’–(a)=-[f(a)+|f(a)|],
由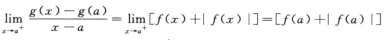
4.设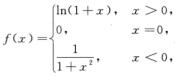 (B)
(B)
A. F(x)在x=0处不连续
B. F(x)在x=0处连续,但不可导
C. F(x)在x=0处可导,且F’(0)=0
D. F(x)在x=0处可导,且F’(0)=1
解析:因为x=0为f(x)的第一类间断点且在x=0处有定义,所以F(x)连续.
由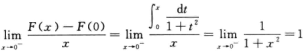 得F’–(0)=1;
得F’–(0)=1;
由
本文档预览:3000字符,共15117字符,源文件无水印,下载后包含无答案版和有答案版,查看完整word版点下载
